
click here for an interactive demo (Click to drag the parts, shift-click to mirror an intersection)
This is an introduction to the system behind Rami, what I'd like to call a drawn programming syntax. What is a drawn programming syntax, and what can it be used for, you might ask? Well, to put it bluntly, I can't see any practical uses where another syntax wouldn't do the job better in all relevant categories, and I've even made a "characterified" version of the syntax in the familiar left-to-right style of most programming languages of today, which does exactly the same. Rami (branches in Latin) is a method of representing a programming or mathematics in a graphical pattern (which here basically means, not written in a line).
Among the motivations for this syntax, is the ability to produce pretty patterns of programming. Another motivation behind some of the choices, although not too relevant for most, is that a hypothetical society in a hypothetical world should be able to use it as their primary display of math/programming. This society should also be able to tweak the display with aesthetics in mind, like how the written word can be made into calligraphy and monograms, although this procedure shouldn't cause it to loose its unambigiousness.
So what does this syntax look like? Let's show example of the mathemathical expression which in python would be written as
y**(4+x+y)/(-x+5)+3
Which in the "characterified" Rami-syntax would be
+( /( +(-(x))(5) )( **( +(4)(x)(y) )(y) ) )(3)
As a quickly made Rami-structure with a swirl it is
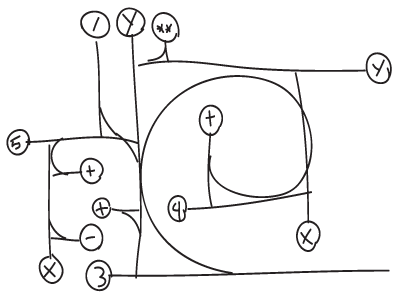
This is also the same expression, although not very polished. Here as a barebone structure, and as a tree drawing over a similar structure, showing a bit more what Rami is named from.

The circles with characters within are just symbols, which could be basically anything, as long as it is known what each symbol represents. Here I've chosen the same symbols as one should be used to from math and programming, in order to make it more easily understood. It is, however, a desire of mine to develop a system for symbols which could fit in nicely among the rest of the structure.
Rami only consists of two graphical and two abstract elements. The graphical elements are the symbols, freely chosen letters, numbers or drawings captured in a circle, and the t-structures ( T ) which combines two graphical elements, representing each of the different abstract elements. Every combination made with a T consists of one value ( v ) and one operator ( op ), and any symbol or another T may represent both, depending on their position within the structure.
The T has three parts, one for value, one for operator and one for output, which is used connect to other structures, and is where one starts when evaluation a structure. Here's an example of a T with a symbol V as value and OP as operator.
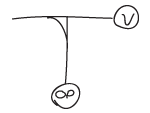
Instead of a symbol at the op- and v-branches of the T, they may lead to another T. To evaluate a ramification, one starts at the output, the empty branch, and follows the line of operators until a dead end is reached. When you reach an end, if the value this operator is combined with is a symbol, evaluate the combination, otherwise, use the same procedure to follow the line and imagine that you are changing the whole T which combined them with a symbol representing the output from the combination. Repeat the process until there's nothing left.
There are faster ways to do it, which are easier as you get into the system. But for a start, and as a very basic example, let's use one iteration this method on a representation of the mathematical expression (3+4)*5. For now, the details of how to produce output from a operator-value combination will be ignored, but the main point here is just the algorithm.
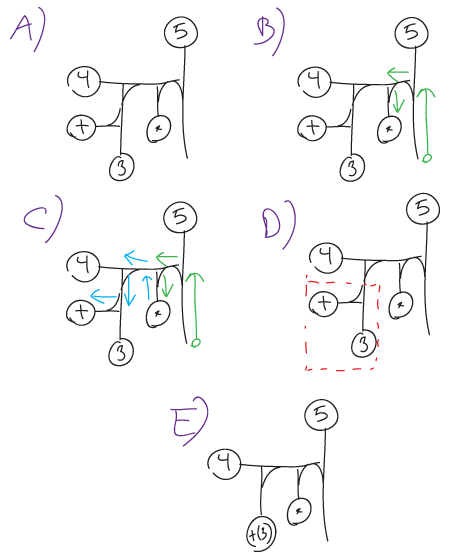
(Badly written text follows)
The first, and perhaps easiest operator to understand would be addition, represented by the + symbol within a circle. It does, however, appear a bit differently from its mathematical counterpart, in that it produces both an operator and a value when combined with a numerical value. + alone is only significant as an operator, and as a value it is evaluated to its identity, 0. When combining + and an arbitrary numerical value x, the resulting +(x) combination will yield simply x as a value. As an operator, the combination +(x) will, when combined with another num. value y, produce the combination +(x)(y), which as a value is x+y, and as an operator it behaves similarly to +(x), only adding y in addition to x and the new value.
From here on, when describing symbols, I will use this notation
symbol := { value | operation }
The value and operation defininitions can be written with math, this symbol notation or pseudo-code. There are two special symbols with special meaning in this notation: v[i] and ø. v[i], or simply vi, refers to the input value combined with the i'th operator from the current scope, v0 can be written as v. ø Is a special empty/undefined/null symbol which doesn't do much and can be defined as
ø := { ø | v[0] } or { ø | v0 } or { ø | v }
Number symbols should be defined as well. A numerical value X is defined as
_X_ := { _X_ | _X_ }
The underscores are added to signify that this isn't an operator X, but a general definition for the value X represents. The addition operator in this notation, would look something like this:
+ := { 0 | { v | { v+v1 | { v+v1+v2 | ... }}}}
Note that the v+v1 in the third scope is the same as v1+v2 in the fourth! The ellipsis implies that it goes on forever in a pattern that should be determinedable by what is shown. It is not a perfect notation, but I have yet to come up anything better.
Some other basic operators that should be defined, are:
- := { 0 | { -v | { -v-v1 | { -v-v1-v2 | ... }}}}
* := { 1 | { v | { v*v1 | { v*v1*v2 | ... }}}}
^ := { ø | { ø | { v**v1 | ø }}}
** := ^
/ := { ø | { ø | { v/v1 | ø }}}
With these mathematical operators, one may now be able to decipher the first two examples.
These are some operators which utilizes some of a computers native functions, and is therefore written in a mix of pseudocode, javascript and the element notation above.
String related operators
chr := { chr | { String.fromCharCode(v) | { chr(v1)+chr(v) | ... } } }
A := { chr | { String.fromCharCode(65+v) | { A(v1)+A(v) | ... } } }
a := { chr | { String.fromCharCode(97+v) | { a(v1)+a(v) | ... } } }
ord := { ord | { v.charCodeAt(0) | { v1.charCodeAt(v) | ø } } }
Usage:
chr(33)(100)(108)(114)(111)(87)(32)(111)(108)(108)(101)(72) -> Hello World
A(-32)(35)(43)(49)(46)(22)(-33)(46)(43)(43)(36)(7) -> Hello World
a(-64)(3)(11)(17)(14)(-10)(-65)(14)(11)(11)(4)(-25) -> Hello World
Assignment
= := {ø | { v | { v1 := v | { v2 := v1 := v | ... } } } }
o := {ø | retrieves value stored as v with = }
+= := {ø | { ø | { =(v1)(v1+v) | ø } } }
-= := {ø | { ø | { =(v1)(v1-v) | ø } } }
++ := {ø | { +=(v)(1) | ø } }
-- := {ø | { -=(v)(1) | ø } }
Usage:
+(=(5)(10))(o(5)) --> 20
+(=(5)(10))(o(5))(++(5)) --> 31
+(=(5)(10))(--(5))(-=(5)(100))(o(5)) --> -163
Comparison
> := { ø | { ø | { v1>v | ø } } }
>= := { ø | { ø | { v1>=v | ø } } }
< := { ø | { ø | { v1<v | ø } } }
<= := { ø | { ø | { v1<=v | ø } } }
== := { ø | { ø | { v1==v | ø } } }
Assorted
seq := { ø | { eval v; return v | { eval v1, v; return v | { eval v2, v1, v; return v | ... } } } }
, := seq
p := { ø | { console.log(v), return v | { console.log(v1,v), return v | ... } } }
P := { ø | { p(v) | { p(v1),p(v) | ... } } }
Special
These operators are special, as they do evaluate their values immediately. They "cut off" the whole branch connected to them as a value, and operates on the branch, rather than the value. Since they are hard to explain using the earlier operator notation, I'll try to explain them with words.
dne := does not evaluate its value before it is used as a value;
u := dne
cond := if/elif/else:
if only one argument, evaluate that arguments wether true or false
if even number of arguments:
evaluates the even(0,2,4,...) arguments as conditionals in an
if/else if sequence, and the odd(1,3,5...) arguments act as
their statements.
if odd number of arguments:
same as above, with the last argument as an else statement
if := cond
while := first argument is condition, the rest is its statement
w := while
Usage:
seq(=(4)(u(++(1))))(=(1)(0))(o(4))(p(o(1)))(o(4))(p(o(1)))(o(4))(p(o(1)))(o(1))
--> 3 (and prints out 1, 2 and 3 in the console)
seq(=(1)(1))(cond(1)(++(1)))(cond(0)(++(1)))(o(1))
--> 2
seq(=(1)(1))(cond(0)(++(1))(--(1)))(o(1))
--> 0
,(=(1)(1))(if(0)(++(1))(0)(--(1))(+=(1)(10)))(o(1))
--> 11
seq(=(1)(4))(w(o(1))(--(1))(p(o(1))))(o(1))
--> 0 (and prints out 3,2,1 and 0 in the console)
(in progress....)